后量子密码学（Post-Quantum Cryptography, PQC）旨在设计能够抵抗量子计算机攻击的加密算法。目前的研究主要围绕以下几类数学难题构建：

---

1. 基于格的密码学（Lattice-Based Cryptography）

核心难题：最短向量问题（SVP）、学习带错误问题（LWE）和环上LWE（RLWE）。

特点：

- 计算效率高，支持同态加密等高级功能。

- 算法结构灵活，可用于加密、签名、密钥交换等。

代表性方案：

- 加密/密钥交换：Kyber（NIST标准化方案）、NewHope、FrodoKEM。

- 签名：Dilithium（NIST标准化方案）、BLISS。

---

2. 基于哈希的密码学（Hash-Based Cryptography）

核心难题：哈希函数的抗碰撞性（如SHA-3、SHA-256）。

特点：

- 安全性依赖于哈希函数的强度，理论成熟。

- 主要用于数字签名，无法直接用于加密。

代表性方案：

- 一次性签名：Lamport签名、Merkle签名。

- 多次签名：XMSS（NIST标准化方案）、SPHINCS+（无状态签名）。

---

3. 基于编码的密码学（Code-Based Cryptography）

核心难题：解码随机线性码（如NP难问题）。

特点：

- 研究历史长（始于McEliece加密方案，1978年）。

- 公钥尺寸较大，但抗量子攻击性强。

代表性方案：

- 加密：Classic McEliece（NIST标准化方案）、BIKE。

---

4. 基于多变量的密码学（Multivariate Cryptography）

核心难题：求解非线性多项式方程组（MQ问题）。

特点：

- 签名速度快，但公钥尺寸大。

- 安全性分析复杂，部分方案已被破解。

代表性方案：

- 签名：Rainbow（NIST第四轮候选，后被攻破）、GeMSS。

---

5. 基于同源密码学（Isogeny-Based Cryptography）

核心难题：超奇异椭圆曲线同源问题（SIDH）。

特点：

- 密钥尺寸小，但计算复杂度高。

- 2022年SIDH部分方案被攻破，安全性存疑。

代表性方案：

- 密钥交换：SIKE（原NIST候选，已因攻击被撤回）、CSIDH。

---

基于格的密码学

格的定义

1. 两种类型的“格”

(a) 序理论中的格（Order-Theoretic Lattice）

• 定义：源于偏序集（poset）的代数结构，其中每对元素都有唯一的上确界（最小上界，join）和下确界（最大下界，meet）。
• 示例：以30的因数构成的集合，在整除关系下形成一个格。例如，2和3的下确界是gcd(2,3)=1，上确界是lcm(2,3)=6。
• 应用领域：逻辑、集合论、抽象代数。与密码学无关。

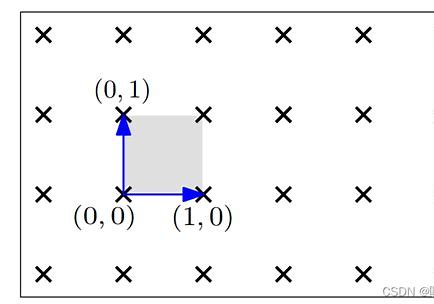
(b) 几何格（点格/整数格）

• 定义：由基向量的整数线性组合生成的n维空间中离散、规则排列的点阵。形式化定义为：

                L={a1​b1​+⋯+an​bn​∣ai​∈Z}
  

  其中b1,…,bnb1​,…,bn​是线性无关的基向量。

• 直观理解：可视为网格交点（例如二维的六边形格），基向量不一定正交。

• 关键性质：

  • 离散性：无聚点。
  • 加法封闭性：对加减运算封闭。

• 应用领域：密码学、编码理论、优化问题。

---

核心难题

最短向量问题（SVP）、学习带错误问题（LWE）和环上LWE（RLWE）。

---

①最短向量问题（SVP）：

给定一个由两个线性无关的向量构成的格子（lattice），即

L={z1​b1​+z2​b2​∣z1​,z2​∈Z},

要求找出非零向量v∈L 使得其欧几里得长度∥v∥最小。

---

具体例子

选取二维格子的基底为

b1​=(4,1),b2​=(2,3).

因此，格子中的任一向量都可表示为

v=z1​(4,1)+z2​(2,3),z1​,z2​∈Z.

---

求解过程

我们尝试通过检查较小整数系数的组合，找出非零向量中模长最小的一个。

1. 考虑 (z1,z2)=(1,0)：

                  v=1⋅(4,1)+0⋅(2,3)=(4,1).
   

模长为

          ∥v∥=42+12=16+1=17≈4.12.

2. 考虑 (z1,z2)=(0,1)：

           v=0⋅(4,1)+1⋅(2,3)=(2,3).
   

   模长为

          ∥v∥=22+32=4+9=13≈3.61.
   

3. 考虑 (z1,z2)=(1,−1)：

            v=1⋅(4,1)+(−1)⋅(2,3)=(4−2, 1−3)=(2,−2).
   

   模长为

                      ∥v∥=22+(−2)2=4+4=8≈2.83.
   

4. 考虑 (z1,z2)=(−1,1)：

                 v=(−1)⋅(4,1)+1⋅(2,3)=(−4+2, −1+3)=(−2,2).
   

   模长同样为 8。

通过比较上述几种情况，我们发现当 (z1,z2)=(1,−1) 或 (−1,1) 时，得到的向量 (2,−2)（或其相反数）具有最短的非零模长，为

                     根号8=2根号2.

---

结论

在给定二维格子

             L={z1​(4,1)+z2​(2,3)∣z1​,z2​∈Z},

中，通过检查小的整数组合，可以得到最短非零向量为

                     v=(2,−2)

（或其负向量），其长度为

                    ∥v∥=22​≈2.83.

总结：这个例子展示了如何利用基本的枚举方法在二维格子中求解最短向量问题。对于高维格子或更复杂的基底，SVP通常会变得计算上十分困难，是密码学和计算复杂性理论中的一个重要难题。