激活函数和损失函数

1.激活函数

激活函数中引入非线性，使神经网络能够拟合复杂的数据分布，解决非线性分类和回归问题。

在回归问题里通常选用ReLu或其变体，在分类问题中隐藏层使用ReLu，输出层使用Sigmoid或Softmax；对于深层网络尽量避免使用容易导致梯度消失的函数，例如Sigmoid和Tanh。

线性层(Linear Layer)，也称为全连接层(Fully Connected Layer)，是神经网络的一个基本构造块，用于实现输入和输出之间的线性变换，通常与激活函数(ReLu,Sigmoid)结合使用，使模型能够学习复杂的非线性映射。

Sigmoid

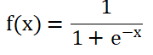
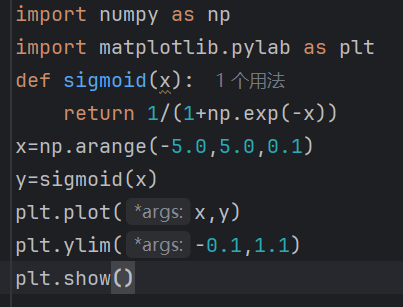
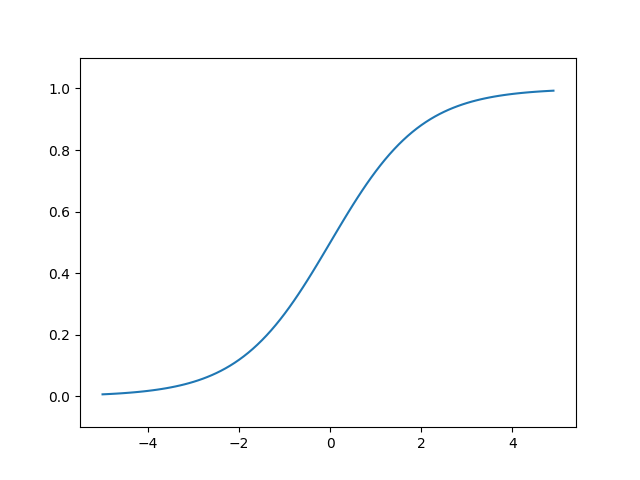
输入以下代码可以实现基础的sigmoid函数图形：

此外，在三层神经网络中sigmoid函数的应用如下：

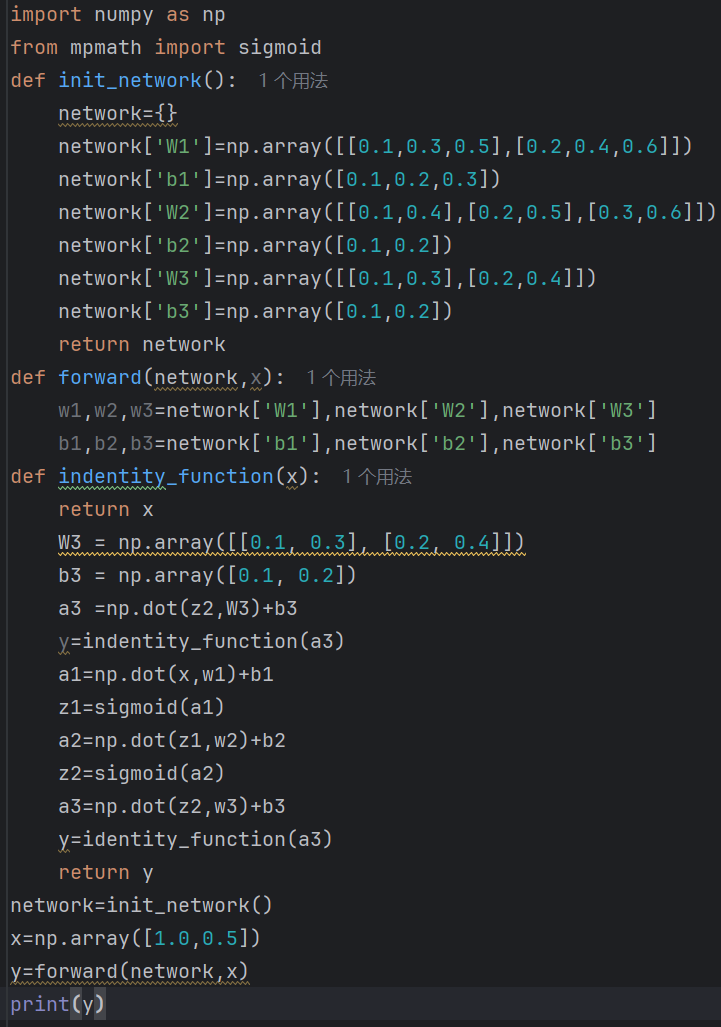
ReLu(Rectified Linear Unit)函数

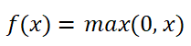
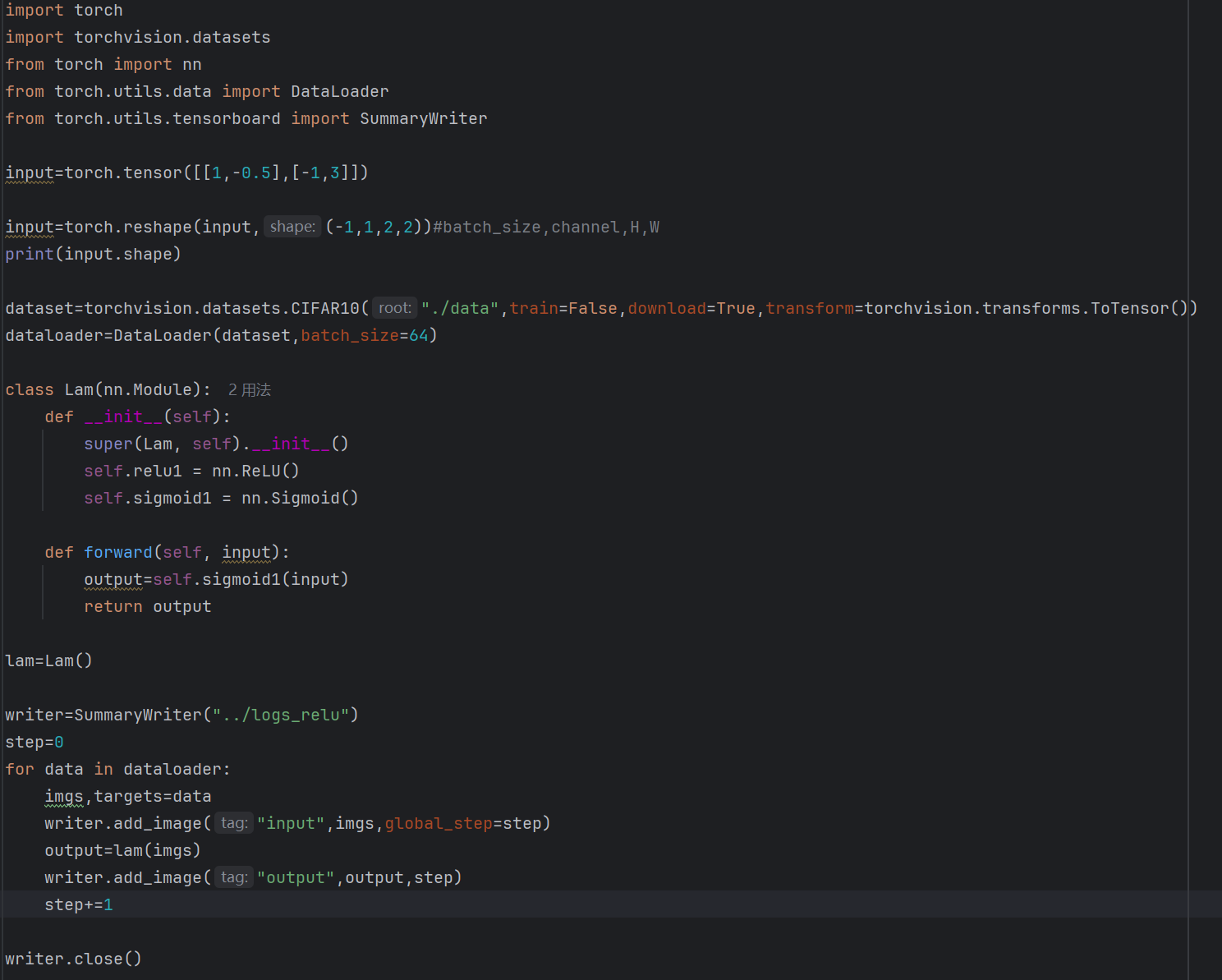
上述的输出结果为torch.Size([1,1,2,2])

2.损失函数(Loss Function)

用于衡量模型的预测值与真实值之间的差异，并以此作为模型优化的目标。损失值越小，说明模型的预测结果和真实值越接近。在训练过程中，模型通常通过优化算法(例如梯度下降)最小化损失函数的值，从而不断更新模型参数，使其对数据的拟合能力更强。

交叉熵衡量两个分布相似性的一种度量方式

交叉熵训练样例及运行结果（先计算softmax再计算交叉熵）

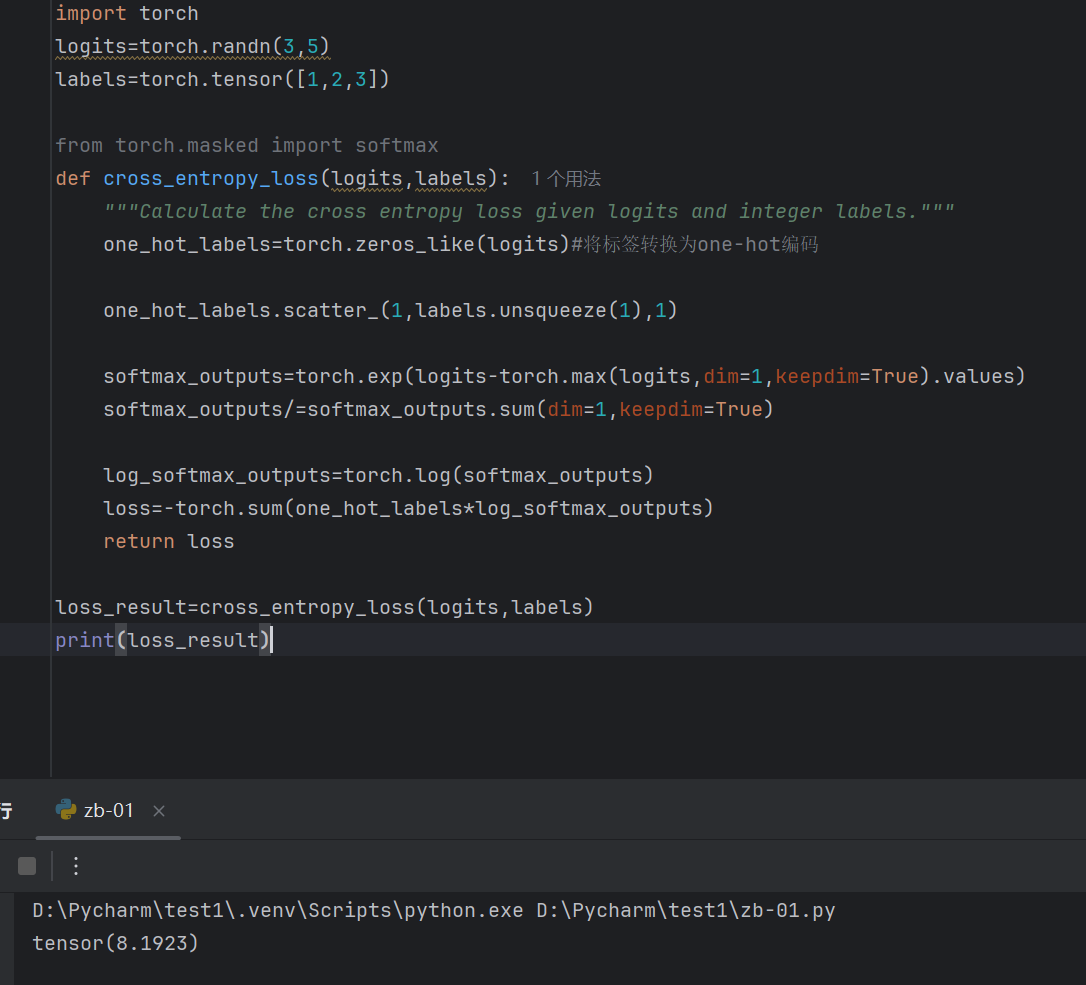
使用损失函数求平均绝对误差，均方误差，交叉熵损失

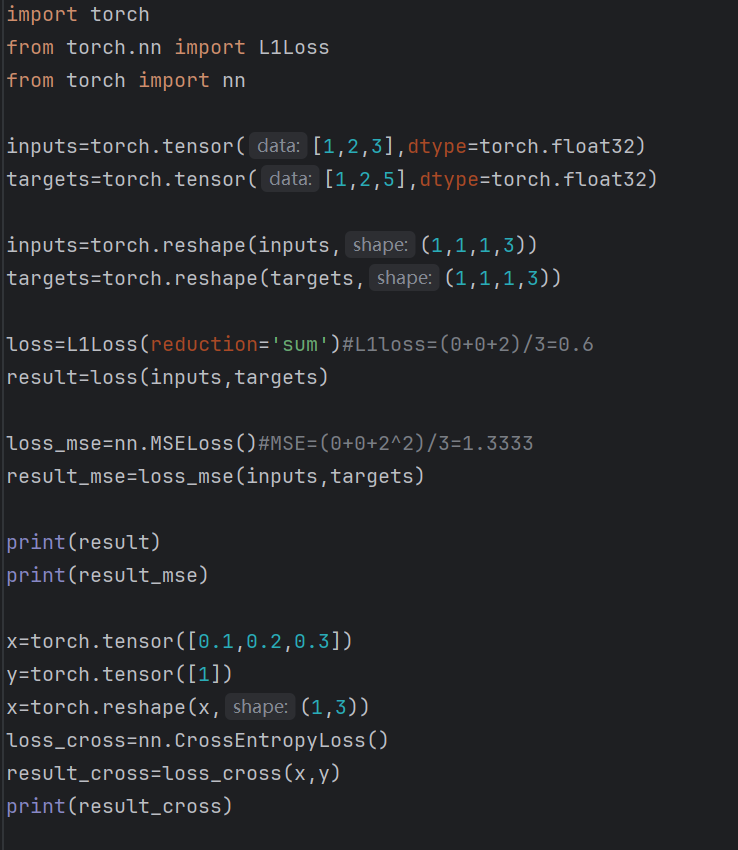
运行结果如下：