前向传播与反向传播

1.前向传播（通过模型计算预测值和损失）
神经网络通过逐层计算，从输入层开始，经过隐藏层，最终到达输出层，以产生预测值的过程。在这个过程中，输入数据通过网络中的权重和偏置进行线性变化，然后通过激活函数进行非线性变换，得到每一层的输出。最终，输出层的输出即为神经网络的预测值。
输入层是神经网络第一层，它接收外部的数据
数据从输入层传递到隐藏层，隐藏层中的每个神经元都会接收来自上一层神经元的输入，并计算加权和。加权和通过激活函数进行非线性变换，生成该神经元输出。
输出层是神经网络的最后一层，它接收来自隐藏层的输入，并计算最终的输出。
下图是进行前向传播的神经网络：

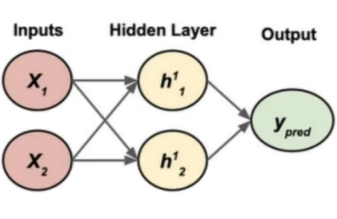
假设：输入值：[0.9,1.0]，目标值：[2.0]
输入到隐藏层的权重W1：W_{1,1}=[0.2,0.3]，W_{1,2}=[0.4,0.5]
隐藏层偏置b_1=[0.1,0.2]
隐藏层到输出层的权重W2：[0.5,0.6]
输出层偏置b_2=[0.4]
下图是带权重、偏置和输出的简单神经网络示意图：

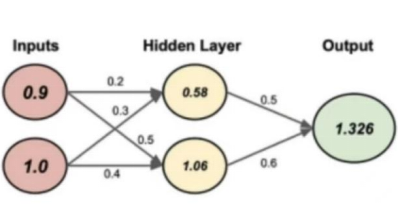
根据这些数据可以进行第一次前向传播：

从输入到隐藏层的线性加权和z1_1，z1_2
Z1_1=W_{1,1}*Input+b_1,1=0.9*0.2+1.0*0.3+0.1=0.58
Z1_2=W_{1,2}*Input+b_1,2=0.9*0.4+1.0*0.5+0.2=1.06
在隐藏层中执行ReLu，得到a1，a2，最后一步是生成输出Z2_1
Z2_1=W2*[a1,a2]+b2=0.5*0.58+0.6*1.06+0.4=1.326

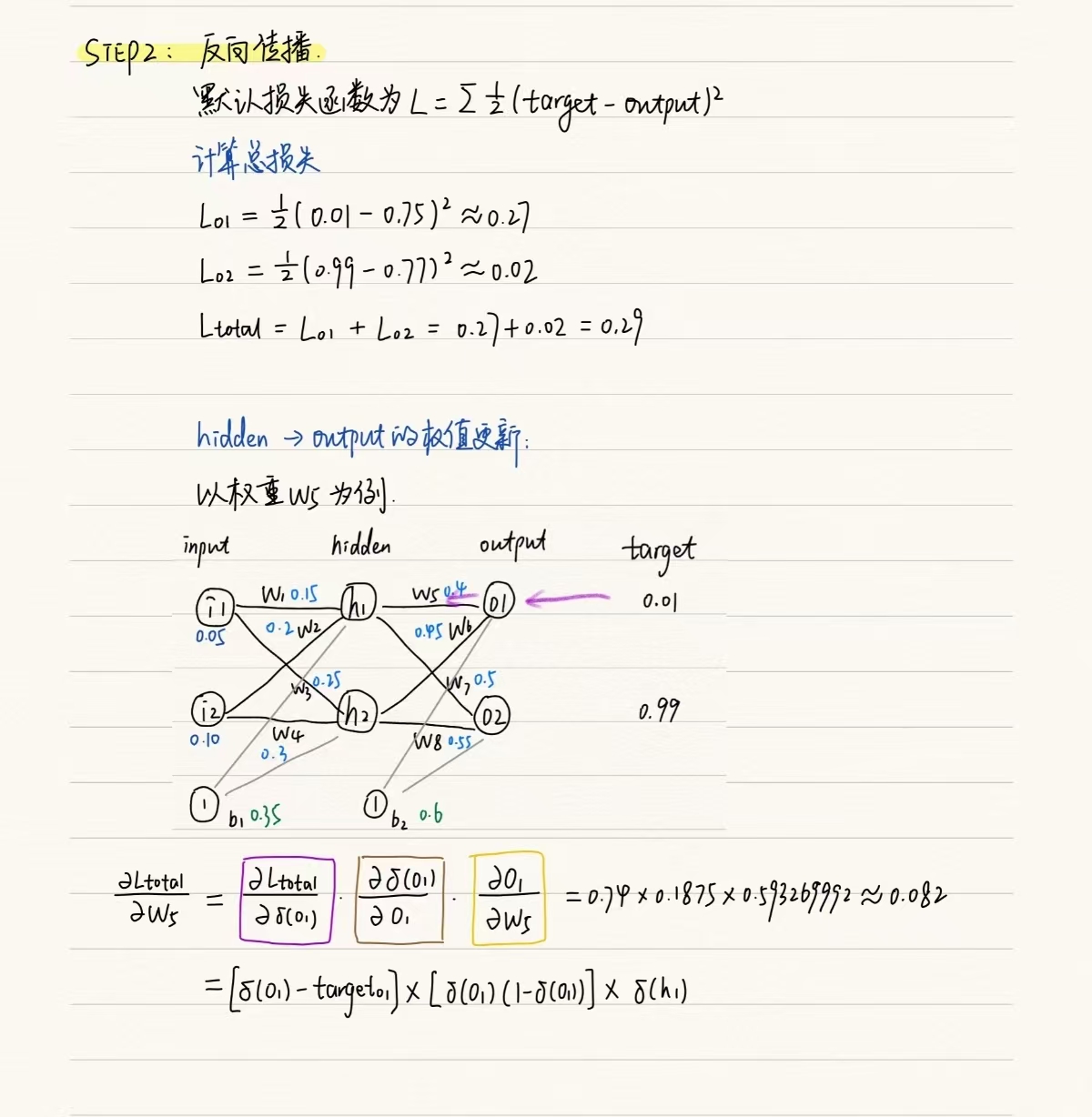
2. 反向传播（利用loss.backward()调用pytorch的autograd模块自动计算梯度，通过优化器optimizer.step()更新模型的参数）

根据损失函数计算梯度，并据此更新网络的权重和偏置。在这个过程中，从输出层开始，使用损失函数逐层计算每个神经元的误差，然后利用这些误差和前一层的激活值来计算当前层权重的梯度（即损失函数对权重的偏导数）。最后使用这些梯度，通过优化算法（例如梯度下降）更新网络的参数，以减小损失函数的值。
计算误差在神经网络的训练过程中，我们需要一个衡量模型预测输出与真实输出之间的差异的标准，这个标准就是损失函数（均方误差MSE，交叉熵损失Cross-Entropy Loss）
计算梯度计算误差后，需要利用链式法则（Chain Rule）将损失函数的值反向传播到网络的每一层，并计算每个权重的梯度。梯度表示了损失函数相对于每个权重的变化率，用于指导调整权重以减小损失函数的值。
更新参数得到每个权重的梯度后，使用梯度下降等优化算法来更新网络的权重和偏置。梯度下降算法的基本思想是沿着梯度的反方向更新权重，以减小损失函数的值。
对于链式法则，先设函数f(x,y,z)=(x+y)z，令q=x+y，那么f=qz
分别求出微分：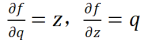

同时q是x和y的求和，可得到: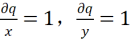
我们需要知道的是: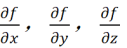
在链式法则中可求得他们的值：

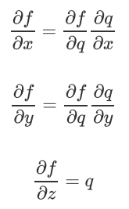
在链式法则中，对其中元素求导我们可以一层一层求导然后将结果乘起来，如下图所示：

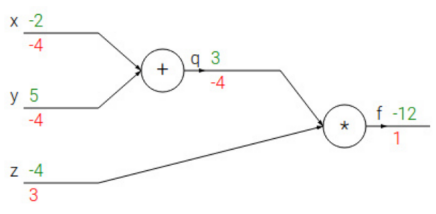
绿色表示数值，红色表示梯度，最开始梯度默认为1



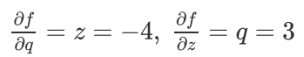
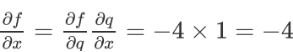
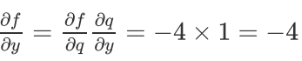
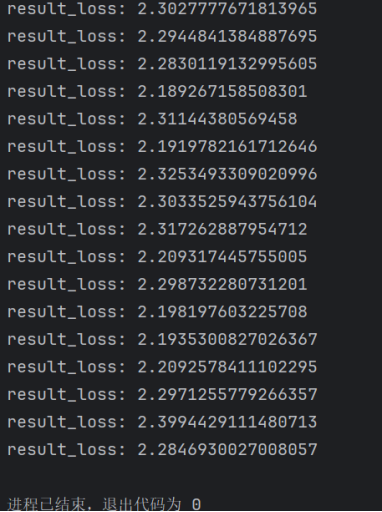
反向传播在CIFAR10中训练并打印每次迭代的损失值：

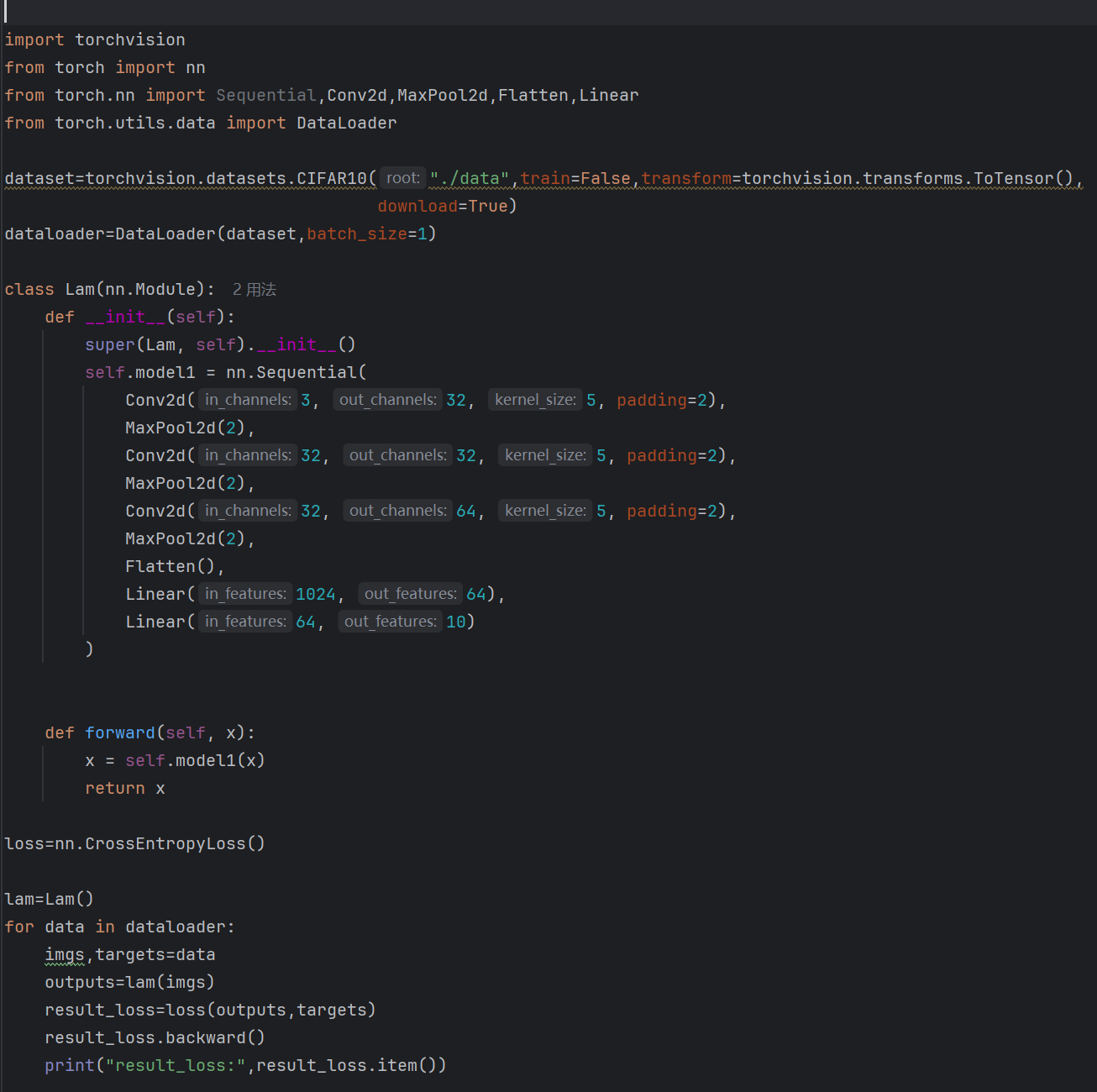
输出的部分结果如下所示：