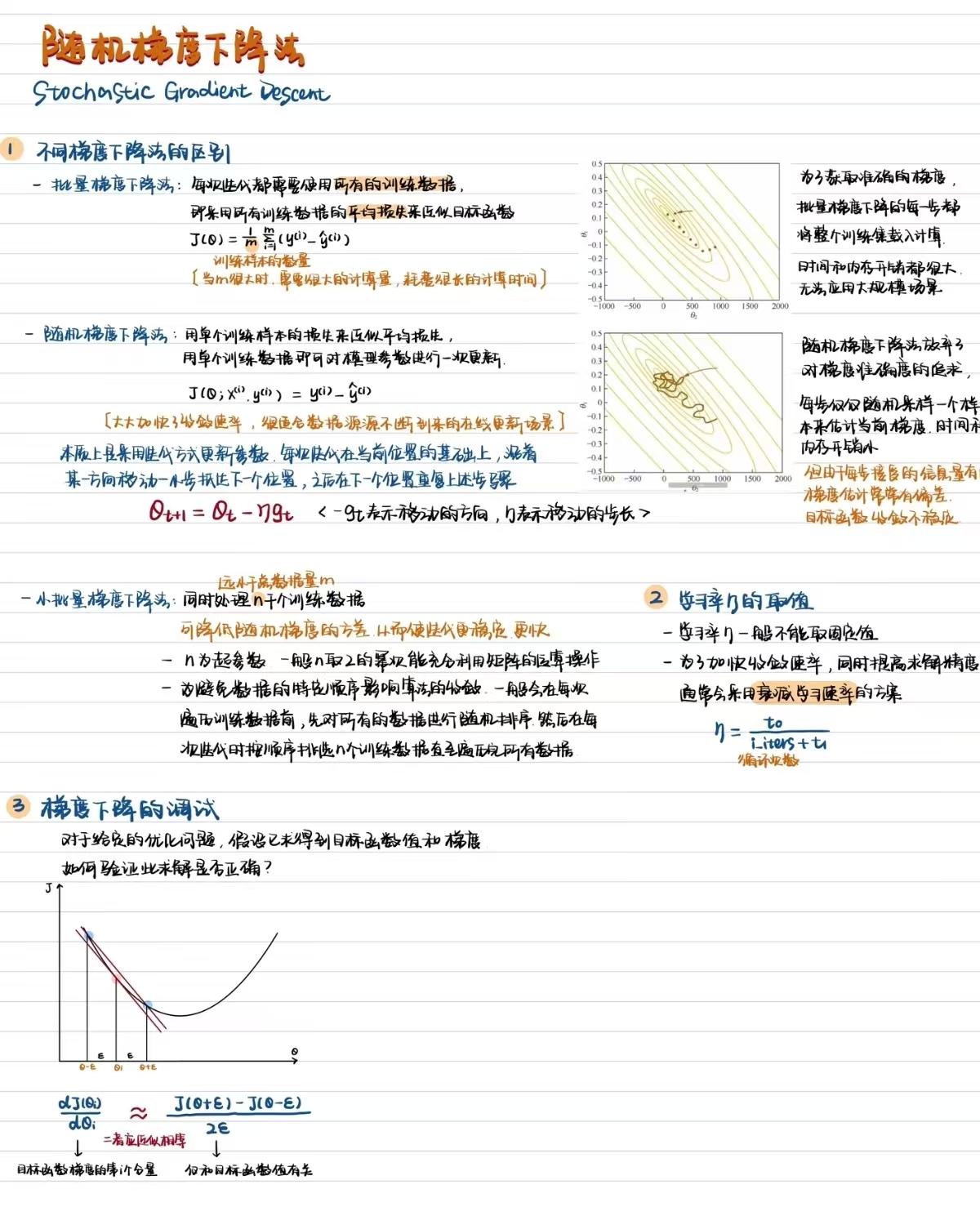
随机梯度下降

1. 线性回归

一元线性回归
变量x_i和目标y_i每个i对应一个数据点，建立模型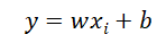

y是我们预测的结果，希望通过y来拟合目标y_i，通俗来讲就是找到这个函数拟合使得误差最小，也就是使其最小化

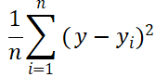
多元线性回归

根据一元线性回归推导出更高层次的模型

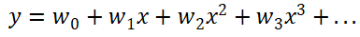
损失函数(均方误差，MSE)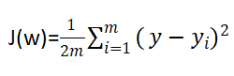
优化方法
正规方程（可以直接用来计算最优解）

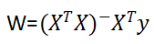
梯度下降（需要调参学习率α）

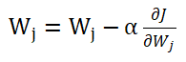
2.梯度下降

梯度在数学上就是导数，如果是一个多元函数，那么梯度就是偏导数。比如一个函数f(x,y),那么f的梯度就是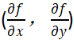可以称为grad f(x,y)。一个点的梯度值是这个函数变化最快的地方，具体来说就是函数f(x,y),在点(x0,y0)处，沿着梯度grad(x0,y0)的方向，函数增加最快，也就是说沿着梯度方向我们能够更快的找到函数的极大值点，那就意味着，反过来沿着梯度的反方向我们能够找到函数的最小值点。
对于梯度下降法，可以举一个例子解释：
当我们在山上的某处位置时，由于我们不知道怎么下山，于是决定走一步算一步，每当走到一个位置时就可以求解当前的梯度，沿着梯度的负方向，也就是当前位置最陡峭的位置向下走一步，然后继续求解当前位置的梯度，如此往复，我们可能会走到山脚，但也有可能我们走到的是局部的山峰低处。沿着梯度的反方向，我们不断改变w和b的值，最终找到一组最好的w和b使得误差最小。在更新的时候我们要决定每一次更新的幅度，也就是此例中下山的步长，这个长度称为学习率，用η表示，学习率太小会导致下降缓慢，太大会导致跳动明显。
通过不断的迭代更新，更新公式是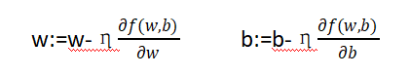梯度下降算法的基本思想是沿着梯度的反方向更新权重，以减小损失函数的值。更新参数得到每个权重的梯度后，使用梯度下降等优化算法来更新网络的权重和偏置。

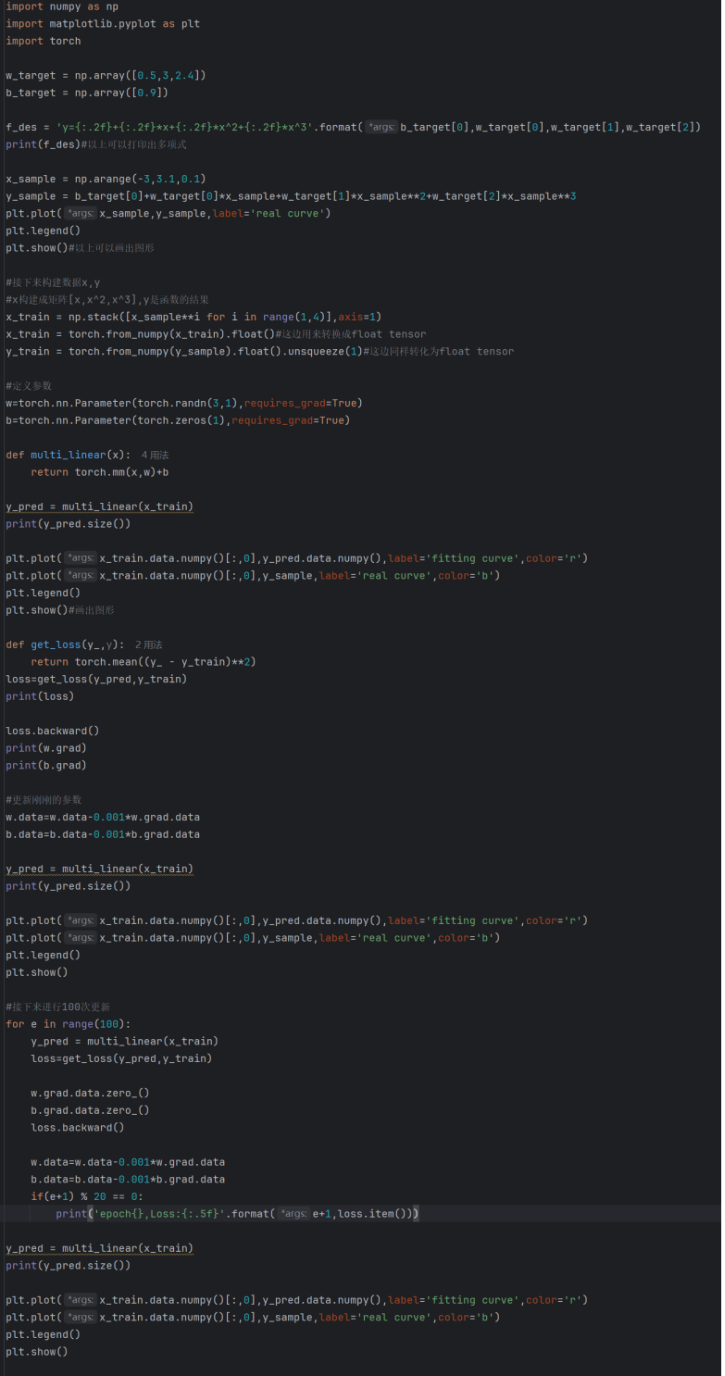
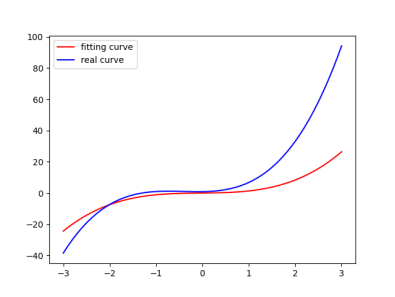
运行结果如下，显而易见在100迭代更新后Loss值已经很小了

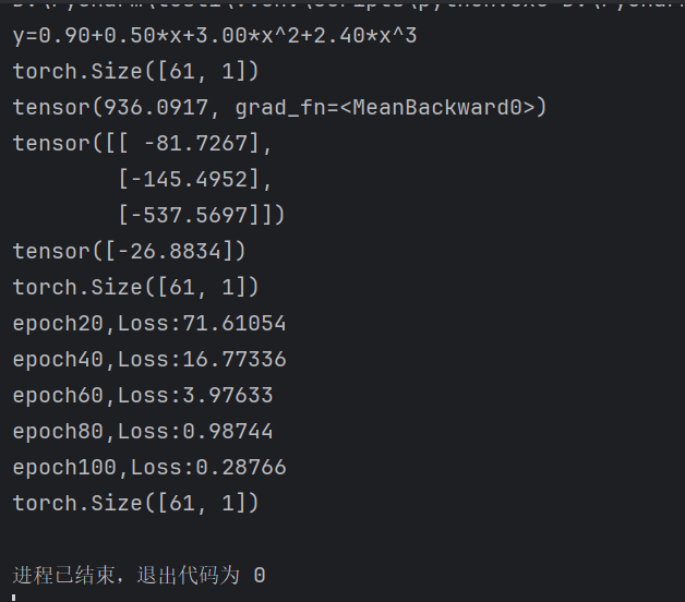
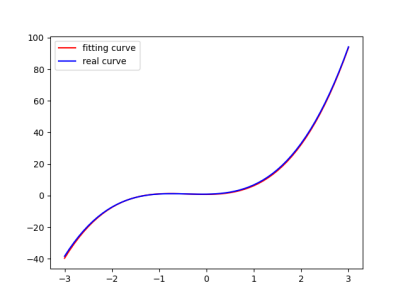
同样的，观察拟合曲线，拟合与真实几乎重合

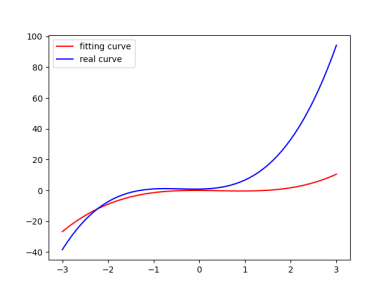
3.随机梯度下降

公式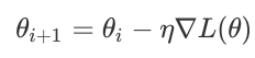先将batch_size设置为1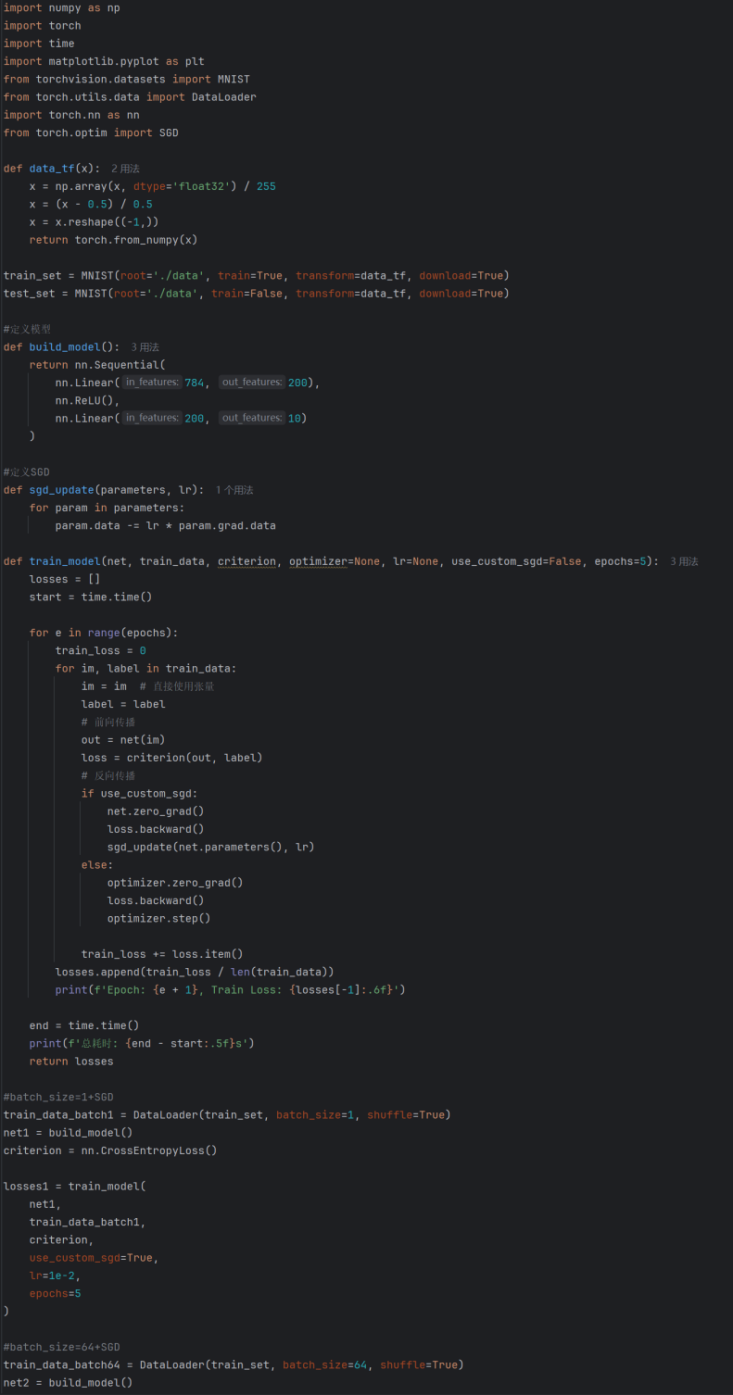
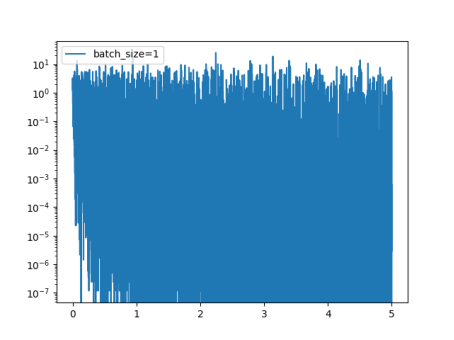
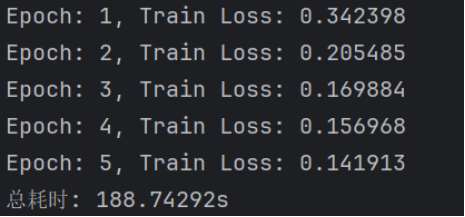
显然loss已经下降到一定的程度，计算的时间也快了非常多。可见batch_size的值越大，梯度就越稳定，batch_size的值越小，梯度就具有越高的随机性。

不难看出loss在剧烈震荡，因为每次都是只对一个样本点做计算，每一层的梯度都具有很高的随机性，而且需要很多运行的时间。
接下来将batch_size设置为64，并使用SGD：


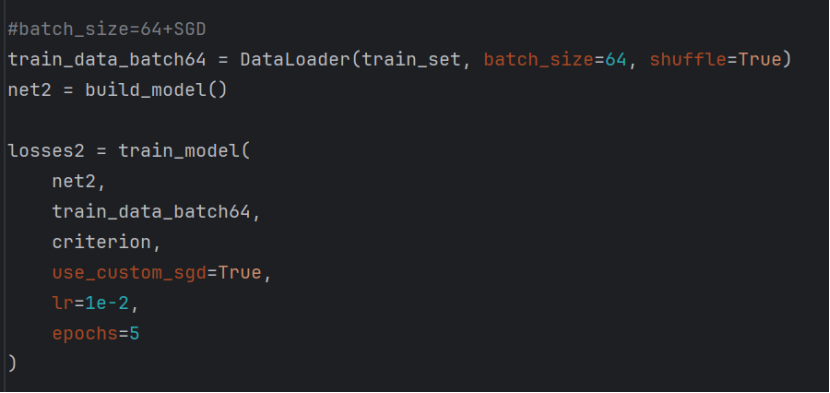
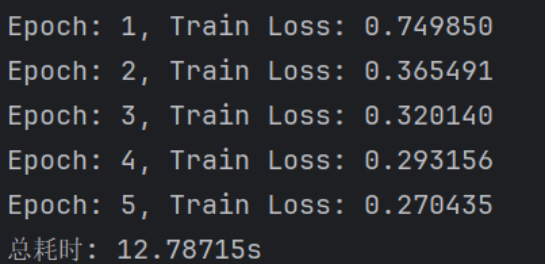
显然loss已经下降到一定的程度，计算的时间也快了非常多。可见batch_size的值越大，梯度就越稳定，batch_size的值越小，梯度就具有越高的随机性。

若使用pytorch自身的SGD则loss与总耗时依旧保持下降趋势

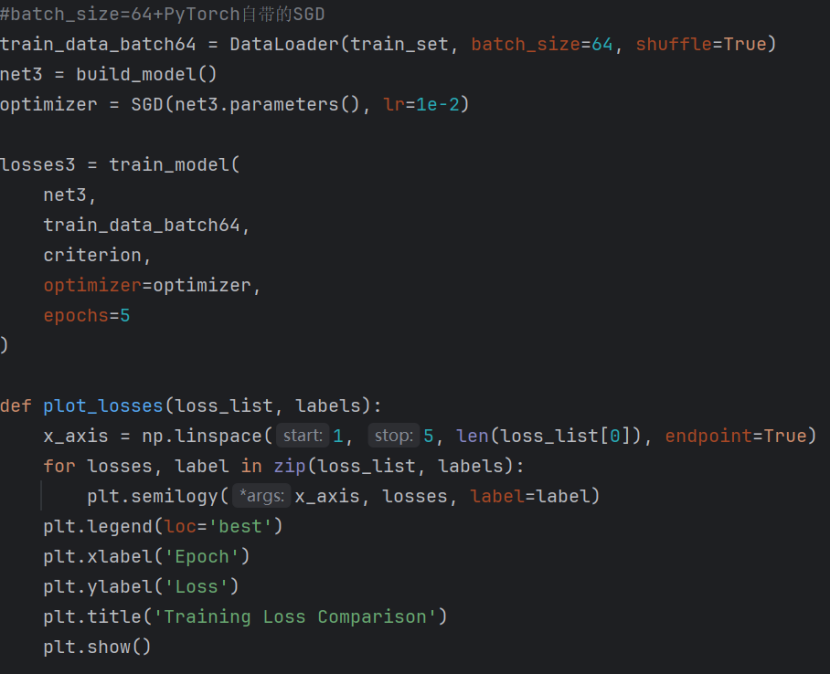
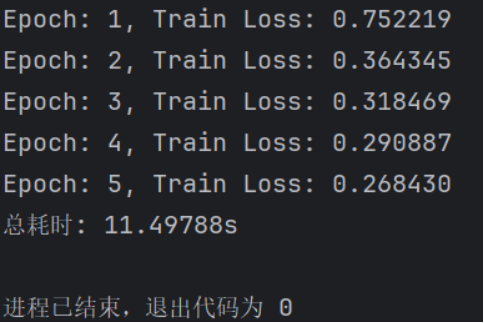
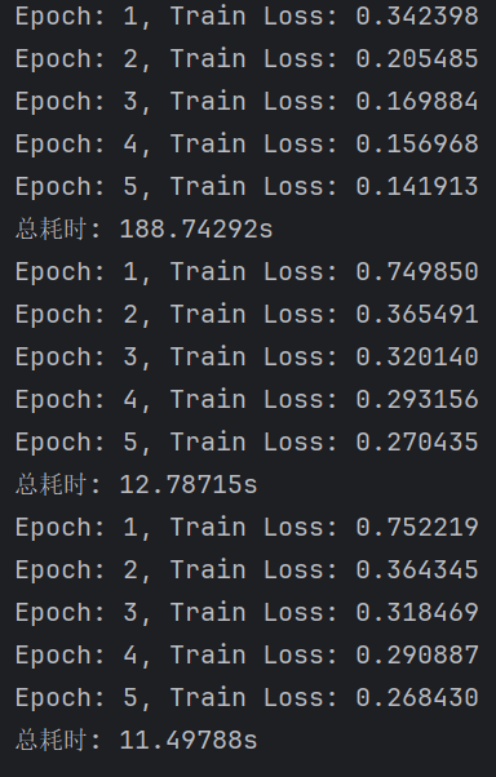
三次运行结果的对比可以看出计算效率提高，但是如果batch_size的值太大，对于内存需求也就更高，不利于网络跳出局部极小点。